RESEARCH ARTICLE
A Differential Evolution Algorithm for Multi-objective Sparse Reconstruction
Xiaopei Zhu1, Li Yan1, Boyang Qu1, *, Pengwei Wen1, Zhao Li1
Article Information
Identifiers and Pagination:
Year: 2022Volume: 1
Issue: 1
E-location ID: e100921196393
Publisher ID: e100921196393
DOI: 10.2174/2666782701666210910170504
Article History:
Received Date: 23/03/2021Revision Received Date: 26/07/2021
Acceptance Date: 05/08/2021
Electronic publication date: 13/12/2022

Abstract
Aims: This paper proposes a differential evolution algorithm to solve the multi-objective sparse reconstruction problem (DEMOSR).
Background: The traditional method is to introduce the regularization coefficient and solve this problem through a regularization framework. But in fact, the sparse reconstruction problem can be regarded as a multi-objective optimization problem about sparsity and measurement error (two contradictory objectives).
Objective: A differential evolution algorithm to solve multi-objective sparse reconstruction problem (DEMOSR) in sparse signal reconstruction and the practical application.
Methods: First of all, new individuals are generated through tournament selection mechanism and differential evolution. Secondly, the iterative half thresholding algorithm is used for local search to increase the sparsity of the solution. To increase the diversity of solutions, a polynomial mutation strategy is introduced.
Results: In sparse signal reconstruction, the performance of DEMOSR is better than MOEA/D-ihalf and StEMO. In addition, it can verify the effectiveness of DEMOSR in practical applications for sparse reconstruction of magnetic resonance images.
Conclusion: According to the experimental results of DEMOSR in sparse signal reconstruction and the practical application of reconstructing magnetic resonance images, it can be proved that DEMOSR is effective in sparse signal and image reconstruction.
1. INTRODUCTION
1.1. Single Objective Sparse Reconstruction
Compressed sensing (CS) [1] is an emerging information acquisition technology, which can reconstruct the original signal from a small number of measured values via the sparse characteristics of the signal. This theory has attracted great attention in the area of information theory, image processing, microwave imaging, pattern recognition, wireless communication and biomedical engineering [2-7]. With the emergence of Big data and the Internet of Things, the application value of the CS theory is increasingly prominent.
According to the CS theory, sparse reconstruction problems can be expressed as Eqs. (1) and (2):
 |
(1) |
where
 is an n-dimensional sparse signal;
is an n-dimensional sparse signal;
 is a m-dimensional measurement vector; A is an
is a m-dimensional measurement vector; A is an
 full-rank and over-complete sensing matrix with
full-rank and over-complete sensing matrix with
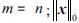 , which is the zero-norm of x, it is used to represents the number of nonzero components of x, and also called the sparsity of the signal x. ᵹ is a non-negative coefficient and represents the noise level.
, which is the zero-norm of x, it is used to represents the number of nonzero components of x, and also called the sparsity of the signal x. ᵹ is a non-negative coefficient and represents the noise level.
It can be proven that these are NP-hard in (1) and (2) [8]. Greedy strategy is a common approach for reconstructing sparse signals. The well-known sparse reconstruction algorithms include basic pursuit algorithm [9], matching pursuit algorithm [10], and orthogonal matching pursuit algorithm [11]. However, these algorithms are difficult to find the global optimal solution, only an approximate solution can be provided as the final solution of the sparse reconstruction problem. In addition, the sparse reconstruction methods based on the regularization framework can also effectively recover the sparse signals. Sparse reconstruction problem can be formulated as Lq regularization problem (Eq. 3):
 |
(3) |
where λ is a non-negative coefficient;
 is a quadratic function for
is a quadratic function for
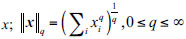 , it stands for the regularization term (Lq-norm of x). q=0, q=1 and q=1/2, which represent the regularization framework based on L0, L1, and L1/2, respectively. Iterative hard thresholding method [12], iterative soft thresholding method [13], iterative half thresholding method [14] are the well-known solvers for L0, L1, and L1/2. Sparsity estimation is often used in these methods, while the sparsity of the practical problems is often unknown. Moreover, the quality of the reconstructed solution is mainly affected by the setting of the regularization parameter λ in the regularization methods. In fact, a sparse reconstruction problem can be transformed into a multi-objective optimization problem and the two objectives are the sparsity and measurement error, which are in conflict with each other. This method avoids the influence of the regularization parameter on the reconstructed solution. The framework of the multi-objective optimization method is given in Eq. (4):
, it stands for the regularization term (Lq-norm of x). q=0, q=1 and q=1/2, which represent the regularization framework based on L0, L1, and L1/2, respectively. Iterative hard thresholding method [12], iterative soft thresholding method [13], iterative half thresholding method [14] are the well-known solvers for L0, L1, and L1/2. Sparsity estimation is often used in these methods, while the sparsity of the practical problems is often unknown. Moreover, the quality of the reconstructed solution is mainly affected by the setting of the regularization parameter λ in the regularization methods. In fact, a sparse reconstruction problem can be transformed into a multi-objective optimization problem and the two objectives are the sparsity and measurement error, which are in conflict with each other. This method avoids the influence of the regularization parameter on the reconstructed solution. The framework of the multi-objective optimization method is given in Eq. (4):
 |
(4) |
where
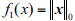 is the sparsity of the sparse signal x
is the sparsity of the sparse signal x
 ; is measurement error.
; is measurement error.
1.2. Multi-Objective Sparse Reconstruction
In recent years, some algorithms based on multi-objective frameworks, MOEA/D and NSGA-II, have been proposed for sparse reconstruction problems. In a study [15], a revised version of MOEA/D based on an iterative thresholding algorithm was proposed. The proposed algorithm is to find a part of the Pareto Front (PF) containing the knee solution, but it is not suitable for multi-objective sparse reconstruction problems with large noise levels. In order to find the optimal tradeoff solution, a multi-objective evolutionary algorithm based on NSGA-II was proposed and defined as StEMO [16]. In StEMO, a soft thresholding algorithm [17] was applied to increase the spread and the convergence rate. In addition, the performance of StEMO is significantly better than the traditional single-objective sparse reconstruction method, and it can recover sparse signals with noisy and noise-corrupted images. The key to a multi-objective sparse reconstruction problem is to quickly and accurately locate the PF near the knee solution. However, the purpose of StEMO is to approximate the entire PF, which consumes a lot of computational resources and ultimately reduces the convergence speed. Li et al. [18] presented a multi-phase multi-objective approach based on decomposition for sparse reconstruction (MOEA/D-L1/2), which optimizes subproblems by multi-phase search strategy. The multi-phase search strategy involves a chain manner in the first phase and a random manner in the second phase, the former aims at approximating the whole PF of the multi-objective sparse reconstruction problem. MOEA/D-L1/2 can effectively solve multi-objective sparse reconstruction problems with or without noise. In order to balance the exploration of the whole PF, the exploitation of the local PF with a k-sparse solution and reducing the computational complexity, a preference-based multi-objective evolutionary approach was proposed in another study [19]. Yan et al. designed a hybrid evolutionary algorithm with linear Bregman-based local search for multi-objective sparse reconstruction problems [20]. In order to accelerate convergence, the number of individuals and iterations in the linear Bregman-based local search is set to be adaptive. A multi-objective sparse reconstruction with transfer learning and localized regularization (MOSR-TLL) was proposed in a study [21]. MOSR-TLL used a knowledge transfer operator and localized regularization strategy to accelerate the convergence rate and improve the reconstruction accuracy. A multi-objective PSO with a one-dimension-dominated method was designed in another study [22], which can find a uniformly distributed PF and improve both the diversity and the convergence of the PF. Multi-objective evolutionary sparse recovery approach based on adaptive local search (ALSEMO) was proposed. Two local search methods are designed using the decomposition-based multi-objective evolutionary algorithm, and an adaptive local search mechanism is formed according to the competition strategy between the two methods in ALSEMO [23]. Most algorithms can solve multi-objective sparse reconstruction problems, and they cost a lot of time on the entire PF. They cannot provide fast reconstruction. However, the solution only close to the knee area is meaningful for the multi-objective sparse reconstruction problem.
Differential evolution (DE) was firstly proposed for continuous global optimization problems [24]. It is a heuristic random search model based on population, which is a branch of evolutionary algorithms. It has the advantages of dynamically tracking the current search situation, less control parameters, high convergence accuracy, strong robustness, and no need to rely on the feature information of the problem. Many multi-objective differential evolution (MODE) algorithms were proposed to solve MOPs. They have been successfully applied in the field of science and engineering [25-29]. They can generate a number of Pareto solutions in a single run; the reason is that most of them are based on population. Furthermore, existing algorithms still need to be improved in terms of convergence speed and reconstruction accuracy. In practical applications, signals or images with noise are also a challenge for multi-objective sparse reconstruction.
To our best knowledge, NSGA-II, MOEA/D and MOPSO, which are popular multi-objective frameworks, have been used for sparse reconstruction problems. MODE is a powerful population-based random search technique, which has the characteristics of simple structure and superior performance. The effectiveness of MODE has been proven in solving complex multi-objective optimization problem. However, it has not been used to solve sparse reconstruction problems. Therefore, this paper proposes a multi-objective differential evolution algorithm for sparse reconstruction problems.
2. METHODOLOGY
2.1. Proposed Algorithm
In order to solve sparse reconstruction problems, a multi-objective differential evolution algorithm is presented, and it introduced an iterative half thresholding algorithm as a local search operator, which can improve the reconstruction accuracy.
2.1.1. Framework of the Proposed DEMOSR
The framework of the proposed DEMOSR is described in Fig. (1), with the corresponding pseudo-code given in Algorithm 1. In Step 1, the initial population P0, the observation matrix A, and the measurement vector y are randomly generated. The objective function values of individuals in the initial population are calculated according to formula (4). PIters is the population of the Iters-th generation. The iteration number is initialized as Iters=1 and the maximum number of the iterations is set to maxIters. In Step 2-Step 3, we use a tournament selection mechanism and differential evolution as mutation and crossover operators to generate a new individual. In order to increase the diversity of solutions, a polynomial mutation strategy is introduced in Step 4. The iterative half thresholding algorithm is introduced as a local search strategy to improve the sparsity of the solution (Step 5). Note that this strategy is used for each individual in the population, including newly generated individuals. In Step 6, the worst individual is removed from the current population PIters. In Step 7, we first sort the sparsity of individuals based on the non-dominant sorting strategy. Then, all non-dominated individuals are selected and the sparsity of the selected individual is updated. In Step 8, the method of the weighted sum of objective values is used to obtain the final solution [30].
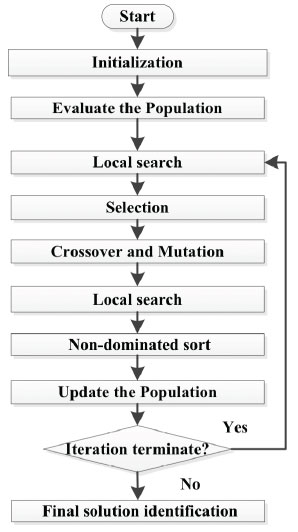 |
Fig. (1). The framework of DEMOSR. |

2.1.2. The Procedure of Initialization of the Sensing Matrix and Measurement Vector
The CS theory mainly consists of three parts: sparse representation, the design of the sensing matrix and sparse reconstruction. The focus of this paper is to design an effective algorithm for sparse reconstruction problems, and the other two parts are not studied in depth. In this subsection, the procedure of initialization of the sensing matrix A and measurement vector y is presented in Algorithm 2.

2.1.3. Selection, Crossover and Mutation Operators
According to the binary tournament selection mechanism, we randomly select two individuals from the population PIters as parents. Then, the DE/rand/1 strategy is applied to generate a new individual which is described as follows (Eq. 5):
DE/rand/1:
 |
(5) |
where
 is the current individual in the Iters generation,
is the current individual in the Iters generation,
 and
and
 are randomly selected from the population of the Iters generation, which are different from each other; r1, r2, r3 are randomly selected from the interval [1, NP], which are also different from each other.
are randomly selected from the population of the Iters generation, which are different from each other; r1, r2, r3 are randomly selected from the interval [1, NP], which are also different from each other.
The new individual is updated in the following way:
If rand<Cr
 |
else
 |
End
 |
where rand is a uniformly distributed random number in [0,1]; the scaling factor F=1; the crossover probability Cr=0.8; ai, bi are the minimum and maximum values of the i-th individual Xi.
In order to increase the diversity of the population, a polynomial mutation strategy [31] is introduced, which is widely used for multi-objective optimization. The polynomial mutation operator is described as follows:
If rand<pm
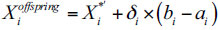 |
else
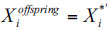 |
End
where pm=1/n and ηm = 20 are the two control parameters for the mutation operator; r=random (0,1);
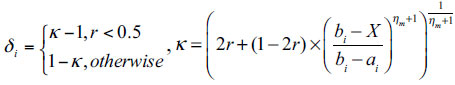 |
The iterative half thresholding algorithm is used to improve the new individual after the crossover operator and mutation operator. The iterative half thresholding algorithm is described in subsection 2.4. After executing the local search strategy, the new individual is merged with the current population, and then the individual with the worse ranks and crowding distances is eliminated via fast-elitist non-dominated sorting and crowding distance criteria [32]. Steps 2-7 are repeated until the termination condition is satisfied. In Step 9, a final solution is selected from the population by the weighted sum of objective values method.
2.1.4. Local Search Operator
The well-known sparse reconstruction methods based on regularization frameworks are iterative hard thresholding algorithm, iterative soft thresholding algorithm and iterative half thresholding algorithm. They are commonly used solvers for L0, L1, and L1/2, respectively. Compared with other thresholding algorithms, the iterative half thresholding algorithm has a faster convergence speed and higher reconstruction accuracy [33]. In DEMOSR, we select the iterative half thresholding algorithm as a local search strategy. The main steps in the iterative half thresholding algorithm are gradient descent, regularization parameter optimization, and truncation operation. The procedure of the iterative half thresholding algorithm is presented in Algorithm 3.

where
 represents the largest element value among the absolute values of all elements in
represents the largest element value among the absolute values of all elements in
 represents the smallest element value among the absolute values of all elements in
represents the smallest element value among the absolute values of all elements in
 represents the maximum number of iterations; the regularization parameter
represents the maximum number of iterations; the regularization parameter
 is an interruption threshold and is set to Ɛ =1E-10. In Step 5,
is an interruption threshold and is set to Ɛ =1E-10. In Step 5,
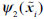 can be formulated as (Eqs. 6 and 7):
can be formulated as (Eqs. 6 and 7):


3. RESULTS AND DISCUSSION
3.1. Experimental Setting
In our experiments, we considered to recover sparse signals and reconstruct the magnetic resonance images. Nine artificial sparse instances without noise (P1-P9) are presented in Table 1. n is the length of signal; m is the length of the observation vector, and k is the sparsity of the true signal. The dimensionality of these instances gradually increases, and the length of the corresponding observation vector gradually decreases. It also indicates that the difficulty of the artificial sparse instances increases gradually.
Considering that the smaller the ratio of m to k, the greater the difficulty of the test instances. The test instances are actually an ill-conditioned problem when the ratio m to k is less than 2. In this case, it is difficult to recover sparse solutions. As shown in Table 1, the test instances P3, P6, and P9 are more difficult to solve than other instances of the same length. DEMOSR is coded by MATLAB and tested on the operating system Windows 10 Professional with 3.60GHz Intel (R) Core (TM) i7-7700 CPU 1170GB memory.
According to the literature [15-16,18], the experimental parameter settings corresponding to each algorithm in this paper are as follows:
MOEA/D-ihalf: step=10;
StEMO: the crossover rate is 0.5 and the mutation rate is 0.1;
DEMOSR: The probability of mating restriction is set to β=0.9; the scaling factor is F=0.9; the crossover probability is set to 1; the polynomial mutation operator is set to pm=1/n and ηm= 20.
For a fair comparison, each algorithm involved in this paper is executed 30 times independently. The parameters of the single-objective sparse reconstruction algorithm (BP, MP, OMP, IST) refer to the settings in the literature [9-11, 17]. The population number of three multi-objective algorithms (MOEA/D-ihalf, StEMO, DEMOSR) is all set to 100. The maximum number of the iterations is 5000. The observation matrix of all algorithms is a Gaussian random matrix, and the measured value vector is generated by y=Ax. The interruption condition of the algorithm is that the number of iterations is greater than or equal to the maximum number of iterations.
3.2. Experimental Results on Artificial Sparse Optimization Instances
In this section, in order to analyze and verify the effectiveness of DEMOSR, the experimental comparisons are made from the reconstruction error with different sparsity and the comparison with two multi-objective algorithms under the same conditions. An evaluation standard (Reconstruction Error, RE) [20] is introduced, which is defined as follows:
 |
(8) |
where xopt stands for the obtained optimal sparse signal; xtrue represents the n-dimensional true signal.
| Instance Name | Length of Signal n | Length of the Observation Vector m | True Sparsity k |
|---|---|---|---|
| P1 | 512 | 300 | 130 |
| P2 | 512 | 280 | 130 |
| P3 | 512 | 260 | 130 |
| P4 | 1024 | 600 | 260 |
| P5 | 1024 | 560 | 260 |
| P6 | 1024 | 520 | 260 |
| P7 | 5120 | 3000 | 1300 |
| P8 | 5120 | 2800 | 1300 |
| P9 | 5120 | 2600 | 1300 |
For the same test instances, the sparsity is determined. When the length of the observation vector m is larger, the smaller the ratio of m to k (the sparsity of the test instance), the greater the difficulty of the test problem, and the true sparse solution or approximate sparse solution is easier to be found. Fig. (2) shows the impact of the length of the observation vector on RE in five sparse methods.
 |
Fig. (2). Comparison of DEMOSR, BP, IST, MP and OMP with different lengths of the observation vector m on RE, where m=250, 260, 270, 280, 290, 300, respectively. |
As shown in Fig. (2), as the length of the observation vector increases, the average value of RE corresponding to each algorithm shows a downward trend, except for OMP. The experimental result is consistent with the theoretical analysis. In addition, this also indirectly shows that the accuracy of the reconstructed solution via OMP and DEMOSR under different lengths of observation vector m is higher than that of other algorithms. However, an atom is selected to update the atom set in each iteration of the OMP, which will cause a huge cost of reconstruction time, especially for the long signals with noise. In addition, the number of iterations is closely related to the number of sparsity or measurement. With the increase of the number of iterations, time consumption will significantly increase. It has a slow speed for image signal reconstruction. In contrast, the diagonal nonlinearity of the threshold operator and the threshold of the function is that the iterative half thresholding algorithm can be applied to large-scale problems. Moreover, it is robust to observation noise. Therefore, we select the iterative half thresholding algorithm as a local search strategy in DEMOSR.
In the areas of sparse reconstruction, a solution has the same or approximate sparsity as the true sparse signal, and the measurement error corresponding to this solution is very small. It can be said that the algorithm successfully reconstructed the true sparse signal. In order to compare the performance of the proposed algorithm MOEA/D-ihalf and StEMO, the simulation experiments are conducted with nine artificial noiseless random sparse signals. The experimental results are shown in Fig. (3).
As shown in Fig. (3), the abscissa represents the sparsity of the test instances, and the ordinate represents the log of the measurement error of the reconstructed signal. It can be seen from (Fig. 3) that the reconstruction solutions obtained by DEMOSR on seven artificial sparse instances (P1, P2, P3, P5, P6, P7 and P8) show a sharp drop near the true sparsity. The smallest measurement errors are all below 1E-10, some are even below 1E-20. For the same instance, MOEA/D-ihalf and DEMOSR have similar phenomena, while the measurement error of the former is larger. Compared with the other two algorithms, the measurement error of the obtained solution by StEMO is not competitive. Therefore, the performance of DEMOSR is better than the other two multi-objective sparse reconstruction algorithms.
To evaluate the performance of MOEA/D-iHalf, StEMO and DEMOSR, we give the statistical results (mean and standard deviation) of the measurement error and the sparsity in the experiments with different test instances. table 2 and 3 show the mean and standard deviation results of the reconstruction error and the sparsity with different test instances, respectively. The numbers given in bold show the results for the best-performing method in each row. Compared with the other two algorithms, the sparsity of the solution obtained by DEMOSR is closest to the sparsity of the true solution. In terms of the measurement error, the statistical results of the mean and standard deviation obtained by DEMOSR are smaller than MOEA/D-iHalf and StEMO. From the statistical results, we can see that StEMO has the largest measurement error on each test instance, indicating that the accuracy of the reconstructed signal is poor. This is consistent with the results observed in Fig. (3).
3.3. Practical Application
In the previous subsection, we compared and analyzed the performance of the proposed DEMOSR with MOEA/D-ihalf and StEMO by simulating nine artificial noiseless random sparse signals. It is worth noting that the research object of these simulation experiments is a set of one-dimensional sparse signals. In order to verify the efficacy of DEMOSR with a practical application and its ability to reconstruct two-dimensional sparse images, we considered to recover magnetic resonance images (SR1, SR2, SR3 and SR4) in this subsection. The magnetic resonance images are 128128, but they are not sparse images. According to the basic idea of compressed sensing, an observation matrix, which is not related to the transform base, can project the magnetic resonance images into a low-dimensional space. Then, the original image can be reconstructed with high probability from these few projections. Based on this, Haar wavelets are used as sparse basis matrix to convert the magnetic resonance images into sparse images.
The original images, the reconstructed spatial images and the reconstructed images by DEMOSR are shown in Fig. (4), and the details of images and measurement errors of reconstructed images are shown in Table 4. The simulation results show that DEMOSR can reconstruct the original image. Compared with the original image, the reconstructed image is clearer. The reconstructed images of SR1 and SR2 contain noise, while the reconstructed images of SR3 and SR4 are more effective and accurate. As shown in Table 4, the measurement errors of SR1 and SR2 are also larger than that of SR3 and SR4. This also further verified the effectiveness of DEMOSR in the image reconstruction, while it is not suitable for the reconstructed magnetic resonance images with noise.
| - | DEMOSR | MOEA/D-ihalf | StEMO |
|---|---|---|---|
| P1 | 129.80.70 | 146.915.35 | 108.69.83 |
| P2 | 129.60.52 | 135.421.92 | 11314.85 |
| P3 | 129.40.84 | 128.17.00 | 113.118.94 |
| P4 | 2600 | 284.135.77 | 202.8914.31 |
| P5 | 2600 | 268.443.85 | 203.215.31 |
| P6 | 259.70.67 | 237.838.50 | 193.118.51 |
| P7 | 1304.15.49 | 1272134.68 | 1516.4363.98 |
| P8 | 1299.79.94 | 1049.4244.88 | 986.2115.41 |
| P9 | 1309.614.10 | 1095205.57 | 846.896.16 |
| - | DEMOSR | MOEA/D-ihalf | StEMO |
|---|---|---|---|
| P1 | 3.93E-061.17E-05 | 1.88E-054.61E-05 | 19.405.39 |
| P2 | 7.52E-061.54E-05 | 1.37E-012.61E-01 | 24.187.55 |
| P3 | 1.40E-024.41E-02 | 1.11E-011.97E-01 | 24.838.66 |
| P4 | 9.35E-072.95E-06 | 2.45E-037.40E-03 | 44.2910.40 |
| P5 | 3.34E-151.06E-14 | 3.32E-019.70E-01 | 59.3318.04 |
| P6 | 6.98E-112.06E-10 | 8.84E-019.43E-01 | 75.1014.72 |
| P7 | 2.87E-058.86E-05 | 8.30E-011.38 | 8.61E-011.60 |
| P8 | 1.10E-043.48E-04 | 4.503.58 | 298.9584.27 |
| P9 | 1.49E-023.53E-02 | 2.89623.7052 | 462.5496.30 |
 |
Fig. (3). Performance of DEMOSR, MOEA/D-ihalf and StEMO on nine artificial sparse instances without noise (P1-P9 correspond to (a-i). |
 |
Fig. (4). The original images, the reconstructed spatial images and the reconstructed images by DEMOSR. |
| Magnetic Resonance Images | Sparsity | Transformed Sparsity | Measurement Error |
|---|---|---|---|
| SR1 | 16266 | 7473 | 2.40E+03 |
| SR2 | 16247 | 7147 | 2.45E+03 |
| SR3 | 8020 | 4524 | 6.37E-05 |
| SR4 | 7806 | 4566 | 1.66E-05 |
CONCLUSION
In this paper, we propose a differential evolution algorithm for solving multi-objective sparse reconstruction problems (DEMOSR), which involves four strategies: tournament selection mechanism, DE operator, polynomial mutation strategy and iterative half-threshold algorithm. The experimental results on nine artificial sparse instances without noise show that the performance of the proposed method is better than MOEA/D-ihalf and StEMO, which are commonly used for sparse reconstruction. It also can be proved that DEMOSR maintains a high exploration ability and convergence rate. Practical applications also prove the effectiveness of DEMOSR in sparse image reconstruction.
For future work, we will conduct more research on improving the ability of DEMOSR to solve sparse reconstruction problems, increasing the robustness of DEMOSR, and reducing the computational complexity of DEMOSR.
CONSENT FOR PUBLICATION
Not applicable.
AVAILABILITY OF DATA AND MATERIALS
All data generated or analysed during this study are included in this published article.
FUNDING
The work has been financially supported by the National Natural Science Foundation of China (61976237, 62001528), the Key Projects of Science and Technology of Henan Province (212102210537).
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
Declared none.




